Applied Mathematics -I(B) papers second semester | Polytechnic paper 2022
Applied Mathematics -I(B)
Time : 3.00 Hours
Maximum Marks : 50
Passing Marks : 17
NOTES :
i) Attempt all Question
ii) Students are advised to specially check the Numerical Data of question paper in both version. If there is any difference in hindi Translation of any question, the students should answer the question according to the English version.
iii) Use of Pager and Mobile Phone by the students is not allowed.
Q.1 Answer any ten parts of the following :
a) Evaluate
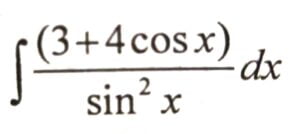
b) Evaluate

c) Define integration by substitution.
d) In which octant point ( 7,-5, -2 ) lie?
e) Find the angle between lines having direction ratios, 1,2,8 and 3, -4,0.
f) define Implicit functions.
g) Evaluate

h) Find the equation of the circle having center at (h, k) and its radius a.
i) Find eccentricity and lat us rectum of the ellipse 2x2 + 5y2 = 20.
j) Find the equation tangent at the point (3, 2) to the ellipse 4x2 + 9y2 = 72
k) Evaluate
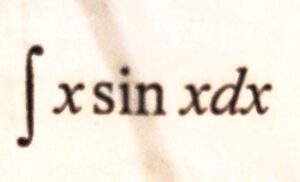
l) Is the equation x2 + y2 + z2 – 10x + 10y + 41 = 0 represent a sphere.
Q.2 Answer any five parts of the following :
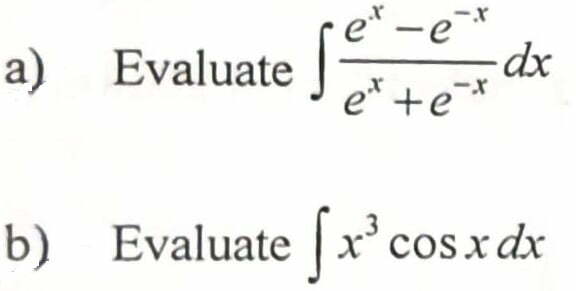
c) Find the length of the arc of the curve y2 = x3 from x = 0 to x= 5/9.
d) Find the equation of normal from the point ( 2, 3 ) to 9x2 + 16y2 = 144.
e) Prove that points A(-1, -2, -3 ), B(1, 1, 1 ) and C(-3, -5, -7) lie in a straight line.
f) Find the equation of sphere whose ends of a diameter are (3, 4, 5) and (5, 2, 3).
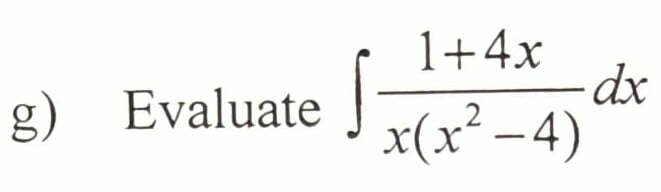
Q.3 Answer any two parts of the following :

b) Find the length of perpendicular from the point (2, 3, 1) to the plane 2x – 3y + 6z + 18 = 0
c) Evaluate
Q.4 Answer any two parts of the following :
a) Prove that
b) Find the area bounded by the curve and axies.
c) Find the equation of tangents from the point (-1, 2) to the parabola x2 + 2x + y = 0 and angle between them.
Q.5 Answer any five parts of the following :
a) Find the volume and surface area of a solid generated by revolving the rectangle about its 12 cm side while the sides of rectangle are 12 cm and 7 cm.
b) Evaluate using Trapezoidal rule.
c) If the coordinates of one end of diameter of the sphere x2 + v2 + z2 – 8x – 12y – 4z + 47 = 0 is (2, 4, 1). Find the coorinates of the other end.
Applied Mathematics -I(B) papers second semester
UP Polytechnic previous year question paper pdf download
Applied Mathematics -I(B) papers second semester, Applied Mathematics -I(B) papers second semester, Applied Mathematics -I(B) papers second semester, Applied Mathematics -I(B) papers second semester, Applied Mathematics -I(B) papers second semester,
ये भी पढ़े …….
- Applied Mathematics-1 question papers 20/01/2022
- पेचकस या स्क्रू डाइवर (Screw Driver) किसे कहते हैं ?
- पेचकस किस धातु का बना होता है ?
- स्क्रू कितने प्रकार के होते हैं ?
- वाइस (Vice) किसे कहते है
- प्लायर्स (Pliers) किसे कहते है ?
- हैमर किसे कहते हैं ?
- हैमर किस धातु का बना होता है ?
- हथौड़ों की औसतन लम्बाई और वजन के बारे में आप क्या जानते हैं ?
- स्पेनर्स किसे कहते हैं ?
- स्पेनर किस धातु के बनाये जाते हैं ?
- सेट स्पेनर किसे कहते हैं ?
- ऐलन की (Allen Key) किसे कहते हैं ?
