applied mathematics 3rd previous year question paper
उत्तर प्रदेश डिप्लोमा
तृतीय सेमेस्टर सॉल्वड पेपर, 2017
अनुप्रयुक्त गणित-II
(APPLIED MATHEMATICS-II)
Total Mark’s: 50
नोट- सभी प्रश्नों के उत्तर दीजिये।
प्रश्न 1. निम्नलिखित में से कोई चार भाग हल कीजिए । ( 4 x 2 = 8)
(अ) यदि 4 =
तो A-1 का मान ज्ञात करो।
उत्तर- यहां A =
दिए गए आव्यूह के सहगुणनखंड निम्नवत् हैं:
A11 = 3, A12 = -1, A21 = -5, A22 = 2
प्रश्न 1. (ब) अवकल समीकरण 
की कोटि तथा घात ज्ञात करो।
उत्तर- दिया गया अवकल समीकरण ….(i)
घात ज्ञात करने के लिए भिन्नात्मक घात को हटाना आवश्यक है।
समीकरण (1) के दोनों पक्षों का घन करने पर,
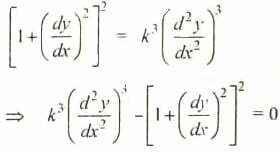
अब,
समीकरण की कोटि = उच्चतम कोटि के अवकल
गुणांक की कोटि = 21
समीकरण की घात = उच्चतम कोटि के अवकल
गुणांक की घात 3
प्रश्न 1. (स) 
का मान ज्ञात करो।
उत्तर- हम जानते हैं कि,
माना s2 + 4 = x
2s ds = dx
sds = dx/2
जब, s = xs, तो x = s2 + 4
प्रश्न 1. (द ) हल करो – (D2 + D – 2) y = e-2x
उत्तर- दिए गए समीकरण का सहायक समीकरण निम्नवत् है:
m2 + m – 2 = 0 [D = m रखने पर ]
m2 + 2m – m – 2 = 0
m (m+ 2) −1 (m + 2) = 0
(m + 2) (m – 1) = 0
m= 1, – 2 वास्तविक तथा असमान मूल
पूरक फलन = C1Ce + C2 e -2x
प्रश्न 1. (इ) दिखाइये कि सदिश (2, 3, 4,) (0, 1, 2,) (–1,1, – 1) एक घात स्वतंत्र है।
उत्तर – माना x1 = ( 2, 3, 4), x2 = ( 0, 1, 2) तथा x3 =(-1, 1,-1)
माना, a1 x1 + a2 x2 +a3 x3 = 0
a1 (2, 3, 4) + a2 (0, 1, 2) + a3 (−1, 1,−1) = (0, 0, 0,)
2a1 + 0a2 – 1a3 = 0
3a1 + 1a2 + 1a3 = 0
4a1 + 2a2 – 1a3 = 0
जो त्रिकोणीय रूप में है।
अब A की कोटि = 3
चरों की संख्या = 3
: A की कोटि = चरों की संख्या
: दिए गए सदिश का एक घात स्वतन्त्र हैं।
प्रश्न 2. आव्यूह A = 
की कोटि ज्ञात करो।
उत्तर- यहां A =
जो त्रिकोणीय रूप में है।
.. A की कोटि अशून्य पंक्तियों की संख्या = 1
प्रश्न 2. ( ब )
का मान ज्ञात करो।
उत्तर-
प्रश्न 2. (स) यदि
तो सिद्ध कीजिए 
प्रश्न 3. निम्नलिखित में से कोई दो हल कीजिये। (2 × 5 = 10)
( अ ) यदि F =xy3 – x3 y तो F का मान ज्ञात करो।
उत्तर- यहाँ F = xy3 – x3y
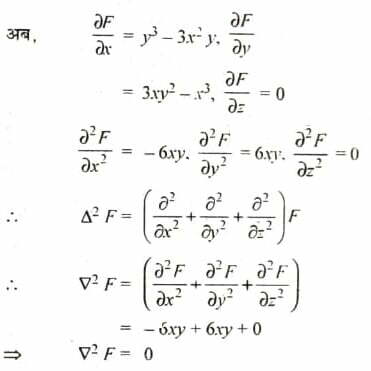
प्रश्न 3. (ब) हल करो- 
उत्तर- दिए गए समीकरण को निम्न प्रकार लिख सकते हैं:
(x2 D2 −2)y = x2 + 1 / x2 ….(1) जहां D = d /dx
.:. L.H.S. के प्रत्येक पद में x व D की घात समान है
.:. यह एक समघात अवकल समीकरण है।
प्रश्न 3. (स) एक द्विपद बंटन में समान्तर माध्य 4 तथा विचरण 2 है तो प्रायिकता ज्ञात करो:
(i) ठीक दो सफलता की।
(ii) कम से कम दो सफलता की।
उत्तर – द्विपद बंटन का समान्तर माध्य =np
तथा विचरण npq
प्रश्नानुसार, np = 4
तथा npq = 2
applied mathematics 3rd previous year question paper
ये भी पढ़े …….