up board class 10 math question paper 12/04/2022




All Question With Answers in Hindi 2022
Answers no -1
(a)-ii
(b)-ii
(c)-i
(d)-i
(f)- iv
Question No2(a)
Solution
2x2+4x+3=0
∴a=2,b=4,c=3
Thus, discriminant of this equation is given by,
D=b2−4ac
∴D=(4)2−4(2)(3)
∴D=16−24
∴D=−8<0
Thus, roots of the equation are imaginary
Question No2(b)
Solution
Given: 15cotA=8
cotA= 8/15 = 1/tanA
= AC/BC
By pythagoras theorem:
AB2 =BC2+AC2
AB2=152+82
AB=289
AB=17
sinA= perpendicular/hypotenuse
= 15/17
secA= hypotenuse/base
= 17/8
Question No2(c)
Solution
A2/A1=(Side2/Side1)2
x2/y2 =A1/A2
x2/y2 =289/ 121
x/y =√289 /√121
x/y = 17/11
Question No2(d)
Solution
relation between mean, median and mode is
mode= 3 median – 2 mean
(mean = 16 mode= 13)
13 = 3 median – 2x 16
13= 3 median-32
13 + 32= 3xmedian
45 = 3x median
45/3 = median
median = 15
Question No3(a)
Then, there exist positive integers a and b such that
3= a/b
Now,
3= a/b
3= a2/b2
3b2=a2
3 divides a2 [∵3 divides 3b2]
3 divides a…(i)
a=3c for some integer c
a2=9c2
3b2=9c2[∵a2=3b2]
b2=3c2
3 divides b2 [∵3 divides 3c2]
3 divides b…(ii)
From (i) and (ii), we observe that a and b have at least 3 as a common factor. But, this contradicts the fact that a and b are co-prime. This means that our assumption is not correct.
Question no 3 (b)
The value of a is 4.
ax + 2y = 2
8x + ay = 4
For infinite solutions,
a1/a2 = b1/b2 = c1/c2
Therefore,
a/8 = 2/a = 2/4
a/8 = 2/4, 2/a = 2/4, a/8 = 2/a
Thus,
a = 4, a = 4, a = 4,-4
Since for infinite solutions all equations should be satisfied simultaneously, therefore a = 4.
Question No3(c)
Solution
We have,
PS/SQ= PT/TR
ST∣∣QR [By using the converse of Basic Proportionality Theorem]
∠PST=∠PQR [Corresponding angles]
∠PRQ=∠PQR [∵∠PST=∠PRQ (Given)]
PQ=PR [∵ Sides opposite to equal angles are equal]
△PQR is isosceles.
Question no 3(d)
Given,
Heightof frustum, h=40 cm
Radius of larger circular end, r1=20 cm
Radius of smaller circular end, r2=11 cm
∴ Slant height, l2=h2+(r1−r2)2
=402+(20−11)2
=1681
=41cm
Hence, the slant height =41 cm
Question 4(a)
HCF(1032,272)= 8
Start with the larger integer, that is 1032, Apply the division Lemma to 1032 and 272, we get
1032 = 272 × 3 + 216
Since , the remainder 216 ≠ 0.
We apply the division Lemma to 272 and 216, we get
272 = 216 × 1 + 56
Remainder 56≠0
216 = 56 × 3 + 48
Remainder 48≠0
56 = 48 × 1 + 8
Remainder ≠ 0
48 = 8 × 6 + 0
The remainder has now become zero ,so our procedure stops.
Since , the divisor at this stage is 8 , the HCF of 1032 is 272 is 8
Question No4(b)
In △ADC and △BAC
∠ADC=∠BAC (Given)
∠C is Common
∴ by AA Criterion of Similarity, △ADC ∼ △BAC
⇒ AD/BA= DC/AC= AC/BC
⇒ DC/AC= AC/BC
∴ CA 2 =CB.CD
Question No4(c)
Steps of Construction :
1- Draw a line segment AB = 5 cm.
2- Draw any ray AX making an acute angle down ward with AB.
3- Mark the points A1,A2,A3,……………A10 on AX such that AA1 = A1A2 = …..= A9A10.
4- Join BA10.
5-Through the point A draw a line parallel to BA10. To meet AB at P Hence AP : PB = 3
Question no4 (d)
Solution:
We will use the basic concepts of trigonometric ratios to solve the problem.
Consider ΔABC as shown below where angle B is a right angle.
cot θ = side adjacent to θ / side opposite to θ = AB/BC = 7/8
Let AB = 7 and BC = 8,
By applying Pythagoras theorem in Δ ABC, we get
AC2 = AB2 + BC2
= (7)2 + (8)2
= 49 + 64
= 113
AC = √113
= √113
Therefore, sin θ = side opposite to θ / hypotenuse
= BC/AC
= 8/√113
cos θ = side adjacent to θ / hypotenuse
= AB/AC
= 7/√113
(1 + sin θ) (1 – sin θ) / (1 + cos θ) (1 – cos θ)
= 1 – sin2θ / 1- cos2θ [Since, (a + b)(a – b)= (a2 – b2)]
= [1 – (8/√113)2] / [1 – (7/√113)2]
= (1 – 64/113) / (1 – 49/113)
= (49/113) / (64/113)
= 49/64
Question NO5 (a)
Let the two consecutive positive integers be x and x+1
Then,
x2+(x+1)2=365
x2+x2+2x+1=365
2x2 +2x−364=0
x2+x−182=0
Using the quadratic formula, we get
x= [−1±√(1+728)]/2
⇒ (−1±27)/2
⇒x=13 and x=−14
But x is given to be a positive integer. ∴x=−14
Hence, the two consecutive positive integers are 13 and 14.
Question NO 5(b)
Solution
Given: (x1,y1 )=(−6,10)
(x2,y2)=(3,−8)
(x,y)=(−4,6)
Using the section formula,we get,
A(-6,10), B(3,-8), C(-4,6)
x= (m1x2+m2x1)/m1+m2
−4=( 3m1−6m2)/ m1+m2
−4(m1+m2) =3m1−6m2
−4m1−4m2=3m1−6m2
−7m1=−2m2
m1/m2 = 2/7
Ratio is 2 : 7.
Hence, the ratio is 2 : 7.
Question No5 (c)
Solution :- As a metallic sphere is melted and recast into the shape of a cylinder, their volume must be the same.
Volume of the sphere = Volume of the cylinde
Let us find the volume of the sphere and cylinder by using formulae;
Volume of the sphere = 4/3πr3 where r is the radius of the sphere
Volume of the cylinder = πr2h where r and h are radius and height of the cylinder respectively
Radius of the sphere, r₁ = 4.2 cm
Radius of the cylinder, r₂ = 6 cm
Let the height of the cylinder be h.
Volume of sphere = Volume of cylinder
4/3πr₁3 = πr₂2h
(4/3)r₁3 = r₂2h
h = 4r₁3 / 3r₂2
= (4 × 4.2 cm × 4.2 cm × 4.2 cm) / (3 × 6 cm × 6 cm)
= 2.744 cm
Hence, the height of the cylinder so formed will be 2.744 cm.
Question NO6 (a)
Solution
We have,
Let the large number is =x
Square of smaller number is =8x
Now, According to given question,
x2−8x=180
x2−8x−180=0
x2−(18−10)x−180=0
x2−18x+10x−180=0
x(x−18)+10(x−18)=0
(x−18)(x+10)=0
x−18=0,x+10=0
x=18,x=−10
x=−10,18
Either
x=−10 and x=18
x=18 is true (Positive value)
Now, square of small number=8x=18×8=144
√144=12
Question No 6 (b)
Side of a square, a=14cm
Radius of each circle, r= 7/2cm
Area of the shaded portion = Area of a square – 4× Area of a circle=a2−4(πr2)
=(14×14−4× 22× 7 × 7 )/28
=196−154
∴ Area of the shaded portion =42cm 2
Question No6 (c)
Solution
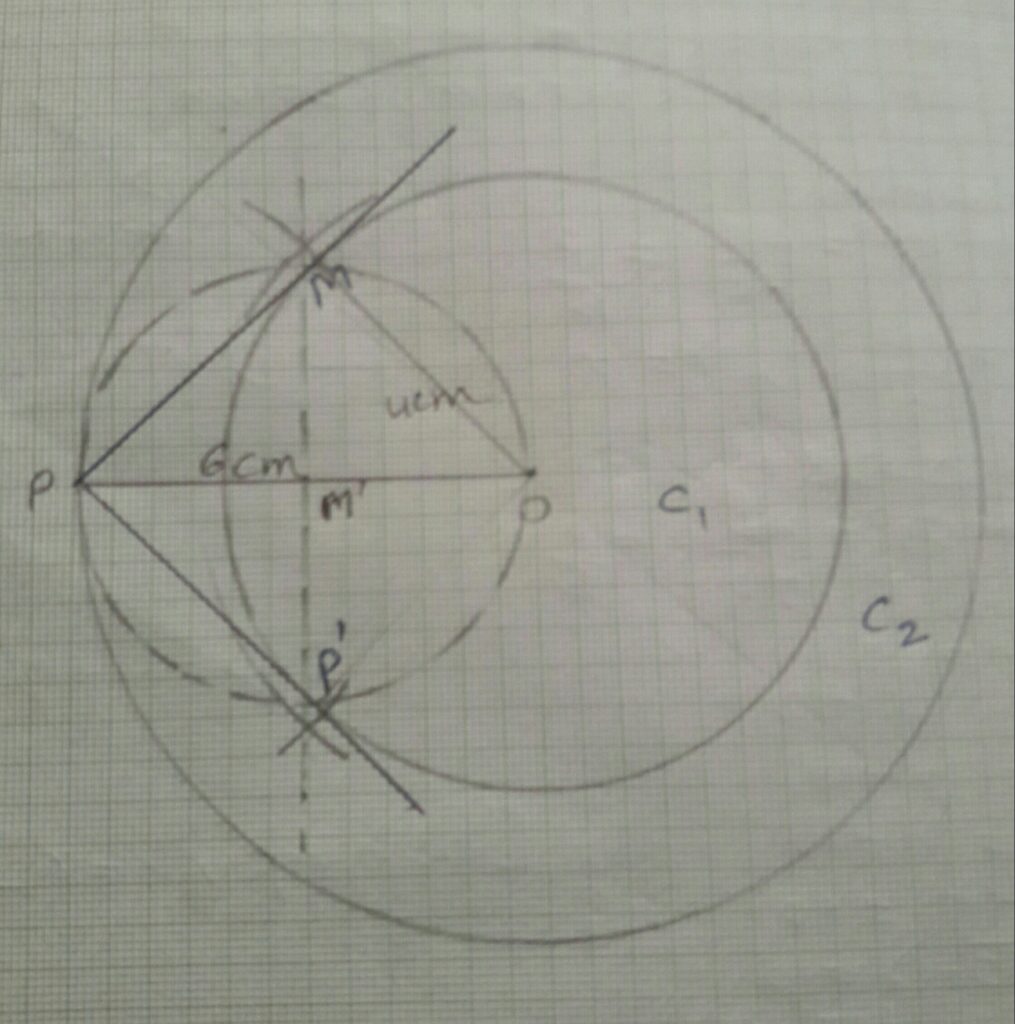
(1)Draw two concentric circle C1and C2with common center 0 and radius 4cm and 6c
(2) Take a point P on the outer circle C2 and join OP.
(3) Draw the bisector of OP which bisect OP at M’.
(4) Taking M’ as center and OM’ as radius draw a dotted circle whichcut the inner circle C1 at two point M and P.
(5) Join PM and PP’. Thus, PM and PP’ are required tangent.
On measuring PM and PP’.
PM=PP′=4.4cm
By calculation:
InΔOMP,∠PMO=90 0
PM2=OP2−OM2 (by pythagoras theorem)
PM2=(6)2 −(4)2
=36−16 = 20
PM2 =20cm
PM= 20
=4.4cm
Hence,
the length of the tangent is 4.4cm
Question No 6 (d)
| Height (in cm) | f | C.F |
| below 140 | 4 | 4 |
| 140 – 145 | 7 | 11 |
| 145 – 150 | 18 | 29 |
| 150 – 155 | 11 | 40 |
| 155 – 160 | 6 | 46 |
| 160 – 165 | 5 | 51 |
N=51⇒N/2 =51/2=25.5
As 29 is just greater than 25.5, therefore median class is 145-150.
Here, l= lower limit of median class =145
C=C.F. of the class preceding the median class =11
h= higher limit – lower limit =150−145=5
f= frequency of median class =18
∴median=145+ (25.5−11×5)/18=145+4.03=149.03
Question No7(a)
let a= 1/(x+y) and b= 1/(x−y)
10a+2b=4 …….1
15a−5b=−2 ……..2
Multiply 1 with 3 and 2 with 2 we get
30a+6b=12 ……3
30a−10b=−4 ……4
subtracting (3) and (4) we get
16b=16
b=1
Substituting b=1 in 1 we get
10a+2×1=4
10a=2
a= 1/5
As
1/(x+y)=a= 1/5
x+y=5…………eq5
and 1/(x−y)=b=1
x−y=1………..eq6
subtracting eq5 and eq6 we get
2x=6
x=3
putting x=3 in eq 5 we get
3+y=5
y=2
hence x=3 and y=2
or
Question No7 (a)
Let Rehman’s present age =x yrs.
3 yrs ago, Rehman’s age =x−3 yrs
5 yrs hence, his age will be x+5 yrs
1/(x−3)+ 1/(x+5)= 1/3
(x+5+x−3)/(x+5)(x−3)= 1/3
x2+2x−15=6x+6
x2−4x−21=0
x2 −7x+3x−21=0
x(x−7)+3(x−7)=0
(x+3)(x−7)=0
x=−3,7
Rehman’s present age is 7 yrs.
Question No7(b)
Let AB and CD be the multi-storied building and the building respectively.
Let the height of the multi-storied building be hm and the distance between the two building be xm
AE=CD=8m [ Given ]
BE=AB−AE=(h−8)m and
AC=DE=xm [ Given ]
Now, in △ACB,
⇒ tan45o=AB/ AC
⇒ 1= h/x
∴ x=h —- ( 1 )
In △BDE,
⇒ tan30o= BE/ED
⇒ 1/√3 = (h−8)/x
∴ x=√3(h−8) —— ( 2 )
⇒ h= √3h−8 √3
⇒ √3 h−h=8 √3
⇒ h( √3 −1)=8 √3
⇒ h= 8 √3/(√3 −1)
⇒ h=[8 √3×8 (√3+1)]/3-1
∴ h=(12+4 √3 )m
∴ x=(12+4 √3)m [ From ( 1 ) ]
∴ The height of the multi-storied building and the distance between the two buildings is (12+4 √3 )m
Or
Question No7(b)
Solution
In ΔBAP
tan30 o = AB/AP
⇒ 1/√3= 10/x
x=10 √3 m
Distance of building
Now,
In ΔPAD
tan45 o= AD/AP
1= AD/AP
⇒x=AD=DB+BA
⇒10 √3=h+10
h=10 √3−10=10( √3−1)
h=10(1.732−1)
h=7.32m
Length of flag.
